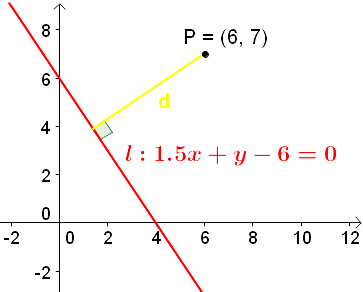
Afstand mellem punkt og linje: \(f(x) = a \cdot x + b\)
Den korteste afstand mellem linjen f(x) og punktet P, er længden af linjen d.
Den kan bestemmes vha. funktionsforskriften og punktet:
\( f \left( x \right) = -1.5 \cdot x + 6 \)
\( P = \left( x_0, y_0 \right) = \left( 6, 7 \right)\)
\( d = \frac{|a \cdot x_0 + b - y_0|}{\sqrt{a^2 + 1}} = \frac{|-1.5 \cdot 6 + 6 - 7|}{\sqrt{\left( -1.5 \right)^2 + 1}} = 5.547 \)
\( P = \left( x_0, y_0 \right) = \left( 6, 7 \right)\)
\( d = \frac{|a \cdot x_0 + b - y_0|}{\sqrt{a^2 + 1}} = \frac{|-1.5 \cdot 6 + 6 - 7|}{\sqrt{\left( -1.5 \right)^2 + 1}} = 5.547 \)