Areal og omkreds
\( A = \pi \cdot r^2 = \frac{\pi}{4} \cdot d^2 = \frac{1}{2} \cdot r \cdot O \)
\( r = radius \)
\( d = diameter \)
Areal og omkreds |
||
| \( O = 2 \cdot \pi \cdot r = \pi \cdot d\) \( A = \pi \cdot r^2 = \frac{\pi}{4} \cdot d^2 = \frac{1}{2} \cdot r \cdot O \) \( r = radius \) \( d = diameter \) | ||
CirkelbueCirkelbuen er den røde del af cirklen til højre. Det er længden af denne man kan udregne |
||
| \( b = 2 \cdot \pi \cdot r \cdot \frac{v}{360^\circ}\) \( b = buelængde \) \( r = radius \) \( v = udsnitsvinkel \) | ||
Cirkeludsnit |
||
Cirkeludsnittet er markeret med blå og bestemmes af udsnitsvinklen og radius på cirklen. |
||
| \( O = 2 \cdot r \cdot \left( 1 + \pi \cdot \frac{v}{360^\circ} \right) \) \( A = \pi \cdot r^2 \cdot \frac{v}{360^\circ} \) \( v = udsnitsvinkel \) \( r = radius \) | 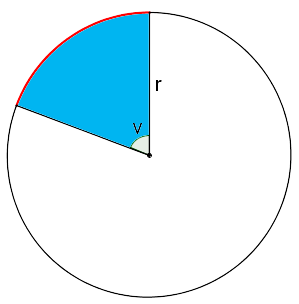 |
|
Cirkelafsnit |
||
Cirkelafsnittet er markeret med rød og bestemmes af udsnitsvinklen og radius på cirklen. |
||
| \( O = 2 \cdot r \cdot \left( \pi \cdot \frac{v}{360^\circ} + \sin\left( \frac{v}{2} \right) \right) \) \( A = \frac{1}{2} \cdot r^2 \cdot \left( \frac{v \cdot \pi}{180^\circ} - \sin \left( v \right) \right) \) \( r = radius \) \( v = udsnitsvinkel \) | ||
Pilhøjde |
||
Pilhøjden er længden af den blå streg på billedet herunder |
||
| \( p = r \cdot \left( 1 - \cos \left( \frac{v}{2} \right) \right) \) \( p = pilhøjden \) \( r = radius \) \( v = udsnitsvinkel \) | ||
Cirkelkorde |
||
Korden er længden af den røde linje på billedet herunder |
||
| \( k = 2 \cdot r \cdot \sin \left( \frac{v}{2} \right) \) \( k = korden \) \( r = radius \) \( v = udsnitsvinkel \) | ||
Cirkelring |
||
| \( O = 2 \cdot \pi \cdot \left( R + r \right) \) \( A = t \cdot m = \pi \cdot \left( R^2 - r^2 \right) \) \( m = \pi \cdot \left( R + r \right) \) \( t = R - r \) \( t = tykkelsen \) \( m = middelomkreds \) | ||